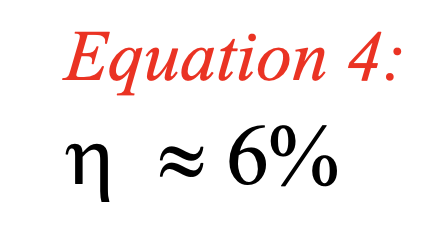Estimates of Second Harmonic Generation (SHG) Efficiency
ESTIMATES OF (SHG) SECOND HARMONIC GENERATION EFFICIENCY
Suppose we want to generate green light at the second harmonic of a 1064 nm pulsed laser, and the laser has a peak power of 10 kW, but an average power is just one Watt. This could be a 10 kHz laser with an energy per pulse of 0.1 mJ and a 10 ns pulse width. A question we’ll address here is this: Can the second harmonic generation be done efficiently with this much peak power? We’ll also analyze what happens with much lower peak power. For example, what if we run the same laser continuously (CW), so the average power might still be one Watt, but the peak power is now also now only one Watt. Can we efficiently generate the second harmonic of that CW beam?
The answers depend upon many details. However, we will make useful estimates of what can be done in a best-case scenario, and we’ll show that the pulsed laser with 10 kW of peak power can efficiently generate green light, unlike the CW version of this laser where the SHG efficiency will be poor. The same method of estimating efficiency can easily be extended to a different crystals and other situations. This example gives insight into what is possible, what is practical, and how the key parameters like the length of the nonlinear crystal, the peak power, and the choice of the nonlinear material affect the SHG efficiency.
To obtain much more accurate calculations, the free software package SNLO by Arlee Smith is a wonderful tool. It runs on Windows computers. For a streamlined version of this for the iPhone, there is an excellent free app, iPhasematch, by Yushi Kaneda.
Figure 1. Second harmonic generation is a nonlinear process. The efficiency often increases nearly linearly with input laser power until reaching about 20%, and then the efficiency starts to saturate more significantly, meaning it doesn’t keep increasing at the same rate. The curve here is meant only to illustrate the behavior of a very well optimized SHG experiment. The maximum efficiency differs with each situation.
How the SHG efficiency scales with key material and beam parameters…
For a nearly-collimated beam in the low power limit (or equivalently the low efficiency limit), the SHG efficiency in a phase matched nonlinear crystal is proportional to the following:
Equation 2 says that the efficiency increases linearly with the power and as the square of the crystal length. Remember, this is in the low power and low efficiency limit. At higher power the efficiency saturates, as illustrated in Fig. 1, and of course efficiency can never exceed 100%. For an approachable reference on these topics of nonlinear optics and nonlinear conversion efficiency, see Fundamentals of Nonlinear Optics by Powers and Haus.
Assumptions…
There are many assumptions that underpin Equation 2. We assume the beam quality is good (M-squared is near 1). We assume the crystal is lossless and homogeneous. We assume that the phase matching is perfect, meaning the crystal orientation and temperature are such that the second harmonic generation adds constructively throughout the crystal. We assume that there isn’t much walkoff (walkoff is discussed in other Gamdan Blogs). We assume the fundamental laser pulse is nearly single-wavelength and that the pulse is long enough that while going through the SHG crystal, dispersion will not cause the beam to spread significantly compared to its pulse length. Picosecond or sub-picosecond pulses can have dispersion problems.
Figure 2. When SHG conversion efficiency is limited by the power in the beam, optimal focusing on the nonlinear crystal (b) keeps the input beam small throughout all of the crystal and optimizes the SHG efficiency. Focusing too tightly (a) or not tightly enough (c) will give larger less intense beams in most (or all) of the crystal and will lower the net nonlinear conversion efficiency.
Scaling of SHG efficiency when the beam is assumed to be optimally focused in the nonlinear crystal…
There is an optimal focusing diameter for the fundamental beam in the nonlinear crystal that produces the maximum SHG power, as illustrated in Fig. 2. Under the assumptions stated earlier, optimal focusing is usually obtained when the depth of focus is about 2/3 of the crystal length, or equivalently the Rayleigh range (the distance from a beam waist to where the mode radius increases by a factor of the square root of 2) is about 1/3 the crystal length. If we use a longer crystal then we want a beam with a longer depth of focus, which must have a larger waist diameter.
For an optimally focused beam, the SHG efficiency is proportional to the following:
Equation 3 uses the same large set of assumptions as Equation 2. The only difference between Equations 2 and 3 is that Equation 3 has efficiency proportional to the crystal’s length, not length-squared. Again, this is because with optimal focusing we adjust the spot size if there are changes in the crystal length. In contrast, Equation 2 is more appropriate if we have a “non-optimal” beam with a diameter that is too large, and we simply look at varying the crystal length, not the spot size. There is more benefit to increasing the crystal length if the beam is already too wide.
Equation 3 is especially useful when evaluating what efficiencies are possible under optimal conditions. If the efficiency number we get here doesn’t meet our needs then we needs, to change our approach.
For a 1 kW fundamental beam with a wavelength of 1064 nm, and with a 1 cm long lithium triborate (LBO) SHG crystal, the conversion efficiency is about 6% with an optimally focused beam. SNLO gives this result, and the experimental results from S.T. Yang et al. (Optics Letters, 1991) corroborate it.
This can be our reference point. Using Equations 3 and 4 together, we can scale from the 6% number to understand the best-case SHG efficiency for other input powers, other crystal lengths, or even other crystals. This will allow us to estimate the input power numbers on the horizontal scale of Figure 1 that give SHG efficiency curves that correspond to different choices of nonlinear crystal material and crystal length. A reminder: this is best case! There are plenty of assumptions stated above, and the efficiency drops if any of those are violated; sometimes it drops drastically.
Estimates of the maximum achievable SHG Efficiency…
The initial question we asked was can SHG be efficient with a 10 kW laser beam. This laser has ten time more peak power than the 1 kW that gave the 6% reference data point of Equation 4. If the LBO crystal is 1 cm long, Equation 3 implies that a 10 kW beam will have 10 times better efficiency than our reference number, so 60%. Sixty percent is high, so there will be saturation—the efficiency won’t really be this high. According to SNLO, the conversion efficiency will be about 39% in this case, which is not small. To do even better, we might want to increase the length of the LBO a bit more, and arrange the LBO and its temperature so there is no walkoff. But, the best-case estimate of 60% conversion efficiency is a useful guide. It shows that there is promise to get significant conversion efficiency from a 1 cm piece of LBO, starting with 10 kW of peak power, and then the challenge is to make sure that our assumptions are mostly met!
Returning to the question of the SHG conversion in the CW example, where the power is 1 Watt (1/1000 kW), Equations 3 and 4 together imply that the efficiency should be (1/1000) 6% or 0.006%. Using Equation 1, the green 532 nm output will be about 60 microwatts. That low power might be useful, depending on the application, but it just isn’t much light. What if we tried a different nonlinear material?
(Here is a good relative reference article from Cornell University: Tunable and efficient ultraviolet generation in nanophotonic lithium niobate)
Conclusion
Starting from the data point shown in Equation 4, and using the scaling from either Equation 2 (for oversized beams) or Equation 3 for optimally focused beams, we can get a quick estimates of the maximum possible efficiency of second harmonic generation for a wide range of crystals and laser beams.
Consult with our in-house team for the best results for your system and application.
One of the things that sets GAMDAN Optics apart is our expert team of scientists and engineers that assist our customers with innovation and discovery of the optimal material for each unique system need. Contact us today for a free consultation.
DR. WILLIAM GROSSMAN, AUTHOR
Will Grossman is a consultant retained by GAMDAN, and his role is to help our customers be more successful with nonlinear optics. His technical expertise includes laser design, nonlinear optics, and laser reliability. Dr. Grossman’s laser designs are used around the world in commercial products. More on the author can be found here.